Regresja logistyczna do klasyfikacji binarnej

Dziś chciałbym zaprezentować Wam przykład zastosowania regresji logistycznej do klasyfikacji binarnej, a to wszystko z użyciem biblioteki Keras. Wiem, że to poprzednie zdanie nie brzmi zbyt zachęcająco 😉 , więc może zacznijmy od podstaw. 

Uczenie maszynowe dzielimy na nadzorowane i nienadzorowane (i jeszcze na uczenie ze wzmocnieniem, ale pomińmy to obecnie). Uczenie nadzorowane to takie, w którym uczymy pewną funkcję przewidywania wyniku na podstawie danych wejściowych, mając do dyspozycji przykładowe pary: dana wejściowa – wynik. Przypomina to uczenie małego dziecka jak wyglądają różne zwierzątka, poprzez wielokrotne pokazywanie mu obrazków i tłumaczenie: “…tu jest piesek, tu konik, to znowu piesek …”. Z kolei uczenie nienadzorowane używa informacji, które nie są sklasyfikowane, czyli nie mają określonych kategorii (wyniku). Celem uczenia nienadzorowanego może być np. podzielenie zbioru danych na kategorie na podstawie podobieństw i różnic, które algorytm automatycznie wychwyci w zbiorze. Dla przykładu można byłoby próbować pogrupować zdjęcia zwierząt w dwie klasy: lądowe i wodne. Odpowiedni algorytm uczenia maszynowego lub sieć neuronowa mogłyby na podstawie wychwyconych cech zwierząt (np. płetwy vs odnóża) rozdzielić je na takie dwie grupy.

Na potrzeby tego posta skupmy się mocniej na uczeniu nadzorowanym. Zawiera ono w sobie dwie kategorie zadań: regresję i klasyfikację. Regresja stara się przewidzieć wartość liczbową (ciągłą), np.: wartość nieruchomości czy kurs akcji. Klasyfikacja na bazie danych wejściowych wyznacza kategorie. Na przykład na podstawie obrazka z ręcznie zapisaną cyfrą, określa jaka to cyfra. 

Regresja logistyczna to uczenie nadzorowane, ale wbrew swojej nazwie nie jest regresją, a metodą klasyfikacyjną – to tak, żeby było ciekawiej 😉 . Zakłada ona, że dane mogą być sklasyfikowane (rozdzielone) poprzez linię lub płaszczyznę n-wymiarową, czyli jest modelem liniowym. Innymi słowy klasyfikacja odbywa się poprzez wyliczenie wartości wielomianu pierwszego stopnia o następującej postaci:

y =ω₁*x₁+ω₂*x₂+…+ω_n*x_n

gdzie x jest daną wejściową, ω wagą przypisaną do tego parametru, a n ilością parametrów wejściowych. Kolejnym krokiem jest przepuszczenie tak uzyskanego wyniku y przez funkcję logistyczną (np. sigmoid lub tangens hiperboliczny), w celu uzyskania wartości z przedziału (0;1). Po uzyskaniu takiej wartości możemy zaklasyfikować daną wejściową do grupy A lub grupy B na podstawie prostej reguły: jeżeli y >= 0.5 wtedy klasa A, w przeciwnym wypadku klasa B.

Proces uczenia maszynowego polega tu na takim doborze wag ω, aby uzyskać na zbiorze uczącym jak największy odsetek poprawnych klasyfikacji. Uzyskuje się to poprzez wyliczenie funkcji błędu oraz jej minimalizację (czyli minimalizację błędu) z wykorzystaniem algorytmu gradientu prostego. 

Posłużmy się przykładem. Załóżmy, że nasze dane, które przygotowaliśmy do uczenia wyglądają tak:

Dość łatwo jest dostrzec, że mamy tu do czynienia z dwoma rodzajami „kropek”: zielonymi i czerwonymi. Co więcej dane wyglądają na dość łatwo separowalne liniowo i w procesie uczenia, wykorzystując np. regresję logistyczną, można nauczyć algorytm separowania tych klas. Wykres funkcji liniowej separującej klasy mógłby wyglądać następująco:

Mając wyuczony klasyfikator moglibyśmy klasyfikować nowe dane, których algorytm wcześniej nie widział. Mogłyby one wyglądać na przykład w taki sposób:

Wyuczony klasyfikator przyjmuje parametry nowych punktów i klasyfikuje je przypisując im wartości (0 ; 0.5), co oznacza klasę „czerwoną” lub wartości [0.5 ; 1) dla klasy „zielonej”.

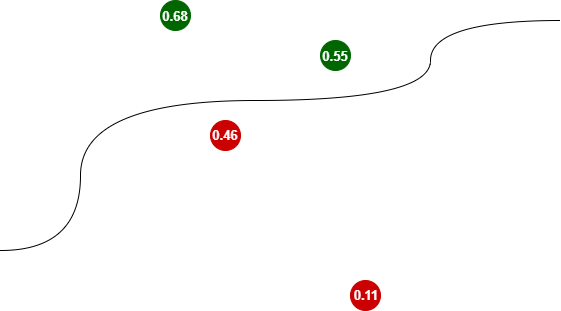
Zauważcie, że im dalej od funkcji separującej, tym klasyfikator jest bardziej „pewny” wyniku. Dla bardziej oddalonej czerwonej kropki wartość jest bardziej zbliżona do zera (0.11), dla zielonej do jedynki (0.68).

Być może brzmi to dość skomplikowanie, ale dostępne biblioteki, w tym Keras, Tensorflow, Theano czy scikit-learn wykonują za nas większość trudnej pracy, w tym wszystkie obliczenia. Mam nadzieję napisać wkrótce post o regresji logistycznej, gdzie przybliżę nieco lepiej to zagadnienie, również od strony matematycznej, ale na tę chwilę powyższe informacje powinny nam wystarczyć, aby zbudować prosty klasyfikator. 

Najczęściej wykorzystywanym typem regresji logistycznej jest regresja binarna, kiedy klasyfikujemy daną wejściową do jednej z dwóch kategorii (stąd nazwa binarna). I takim zagadnieniem zajmiemy się w dalszej części posta. Skorzystamy ze zbioru MNIST, o którym szerzej pisałem w tym poście.

Zbiór MNIST posiada jednak 10 klas i będziemy musieli go ograniczyć do dwóch, co samo w sobie jest ciekawym ćwiczeniem programistycznym.

Ok, dosyć tego wstępu teoretycznego, do dzieła! 😎

Jeżeli potrzebujesz zbudować środowisko programistyczne, w którym będziesz mógł realizować prace opisane w tym poście, zapraszam do zapoznania się z postem Środowisko programistyczne dla uczenia maszynowego.

Na początek importujemy numpy oraz bibliotekę Keras i wyświetlamy jej wersję.

import numpy as np
from tensorflow import keras
print (keras.__version__)
>>> 2.2.4-tf

Ze zbiorów danych, jakie są zawarte w bibliotece Keras, importujemy MNIST. Jeżeli potrzebujecie więcej informacji o zbiorze MNIST rzućcie okiem na ten post.

from keras.datasets import mnist

Importujemy dane do zmiennych i sprawdzamy ich kształt.

(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train.shape
>>> (60000, 28, 28)
y_train.shape
>>> (60000,)

Sprawdźmy pierwsze 10 etykiet.

y_train[0:10]
>>> array([5, 0, 4, 1, 9, 2, 1, 3, 1, 4], dtype=uint8)

Jak widać zawierają one różne cyfry. A nas interesują tylko dowolne dwie z nich, gdyż chcemy przeprowadzić binarną klasyfikację, czyli podział na dwa zbiory. Zajmiemy się jedynkami i zerami, ale możecie wybrać dowolną parę cyfr. Używając małej sztuczki programistycznej tworzymy nowe zmienne, do których trafiają jedynie zera i jedynki.

x_train_new, y_train_new = x_train[(y_train==0) | (y_train==1)], y_train[(y_train==0) | (y_train==1)]

Sprawdźmy jaki kształt mają nowe zbiory danych.

x_train_new.shape
>>> (12665, 28, 28)
y_train_new.shape
>>> (12665,)

Jak widać, mamy podzbiór 12665 elementów (tylko zera i jedynki) wybrany z pełnego zbioru, który zawiera 60000 elementów (wszystkie cyfry). Aby upewnić się, że faktycznie mamy tylko zera i jedynki, wyświetlmy na nowo pierwszych 10 etykiet.

y_train_new[0:10]
>>> array([0, 1, 1, 1, 1, 0, 1, 1, 0, 0], dtype=uint8)

Jest dobrze! 🙂 Zbiór MNIST dostarcza dane w formie obrazków o rozdzielczości 28 x 28 pikseli. W konsekwencji zmienna x_train_new jest trójwymiarową tablicą danych, w której pierwszy wymiar jest indeksem zbioru, a pozostałe dwa wymiary zawierają właściwe dane każdego obrazka. Dla potrzeb uczenia maszynowego potrzebujemy jednak spłaszczyć dane do dwóch wymiarów: indeksu i danych spłaszczonego obrazka (28 * 28 = 784).

x_train_final = x_train_new.reshape((-1, 784))
x_train_final.shape
>>> (12665, 784)

Analogiczną sekwencję operacji musimy wykonać dla zbioru testowego.

x_test_new, y_test_new = x_test[(y_test==0) | (y_test==1)], y_test[(y_test==0) | (y_test==1)]
x_test_new.shape
>>> (2115, 28, 28)
x_test_final = x_test_new.reshape((-1, 784))

Ostatnim elementem przygotowania danych jest ich normalizacja.

x_train_final = x_train_final / 255
x_test_final = x_test_final / 255

Mając dane w czterech finalnych zmiennych: x_train_final, y_train_new, x_test_final oraz y_test_new, możemy przejść do tworzenia modelu. Korzystamy z modelu keras.Sequential i definiujemy tylko jedną warstwę, która będzie przyjmować na wejściu obrazek (o wielkości 784), wyliczać wartość wielomianu: x1 * w1 + x2* w2 + … + x784 * w784,a następnie przepuszczać wynik przez funkcję sigmoid, która ściśnie go do przedziału (0;1).

model = keras.Sequential({
   keras.layers.Dense(1, input_shape=(784,), activation='sigmoid')
})

W kolejnym kroku Keras oczekuje skompilowania modelu poprzez wywołanie metody compile. W tym kroku specyfikuje się:

• rodzaj optymalizatora: stosujemy metodę stochastycznego spadku wzdłuż gradientu
• funkcję obliczającą stratę / koszt: Keras oferuje wiele różnych funkcji kosztu. W naszym przypadku najodpowiedniejszą funkcją będzie binary_crossentropy
• opcjonalnie można zdefiniować metrykę, która będzie śledziła postępy uczenia

model.compile(optimizer='sgd', loss='binary_crossentropy', metrics=['binary_accuracy'])

Model jest obecnie gotowy do nauki. Aby ją rozpocząć wywołujemy metodę fit, przekazując jej następujące dane:

• dane zbioru uczącego, wraz z labelkami
• liczbę epok, która wskazuje ile razy zbiór uczący ma być wykorzystany w fazie uczenia – tu przerobimy go 5 razy. Można spokojnie zmieniać ten parametr, aby poeksperymentować, ale raczej nie będzie miał on dużego wpływu na wynik. W tym sensie, że nawet ustawienie go na 1 może dać niezłe efekty uczenia, a ustawienie go na bardzo dużą wartość nie poprawi istotnie wyniku, a na pewno wydłuży obliczenia i może doprowadzić do overfittingu
• czy wymieszać dane przed przejściem do kolejnej epoki (silnie zalecane)
• oraz batch_size. Ten parametr określa ile próbek danych wykorzystywanych jest do wyliczenia aktualizacji gradientu. Przetwarzanie w paczkach znacząco przyspiesza obliczenia, bo gradient jest obliczany jedynie dla danej paczki, a nie dla całego zbioru.

model.fit(
   x=x_train_final,
   y=y_train_new,
   shuffle=True,
   epochs=5,
   batch_size=16
)

>>> Epoch 1/5
>>> 12665/12665 [==============================] - 1s 93us/sample - loss: 0.0828 - binary_accuracy: 0.9853
>>> Epoch 2/5
>>> 12665/12665 [==============================] - 1s 92us/sample - loss: 0.0213 - binary_accuracy: 0.9972
>>> Epoch 3/5
>>> 12665/12665 [==============================] - 1s 96us/sample - loss: 0.0154 - binary_accuracy: 0.9975
>>> Epoch 4/5
>>> 12665/12665 [==============================] - 1s 95us/sample - loss: 0.0127 - binary_accuracy: 0.9976
>>> Epoch 5/5
>>> 12665/12665 [==============================] - 1s 76us/sample - loss: 0.0111 - binary_accuracy: 0.9977

Jak widać już po pierwszej epoce metryka wskazuje na 98.5% poprawności. Po pięciu epokach mamy 99.77%. Prawdziwym jednak testem dla algorytmu uczącego się jest oczywiście weryfikacja nauki na zbiorze, którego algorytm wcześniej nie widział. W naszym przypadku będzie to zbiór x_test_final i jego labelki y_test_new.

eval = model.evaluate(x=x_test_final, y=y_test_new)
>>> 2115/2115 [==============================] - 0s 51us/sample - loss: 0.0065 - binary_accuracy: 0.9995
eval
>>>  [0.006539232165791561, 0.9995272]

Co ciekawe, uzyskaliśmy jeszcze lepszy wynik – na poziomie 99.95%. Zapiszmy więc model do pliku.

model.save(r'./logisticRegressionKeras.hdf5')

Gotowi na więcej? Świetnie! 😎 

Skoro zapisaliśmy model do pliku, to można z niego skorzystać w dowolnym innym notebooku. Poniżej pokażę, w jaki sposób można tego dokonać, a przy okazji zrobimy również mały, można powiedzieć domowy eksperyment 😉 z rozpoznawaniem przez wyuczony model mojego ręcznego pisma. Ale zaczynimy od niezbędnych importów (pamiętajcie, że zakładam pracę w nowym notebooku, więc importy są konieczne).

import numpy as np
from tensorflow import keras
from PIL import Image
from matplotlib.pyplot import imshow
%matplotlib inline

Ładujemy model z pliku do zmiennej model, korzystając z funkcji load_model().

model = keras.models.load_model(r'./logisticRegressionKeras.hdf5')

Na początek sprawdźmy, czy nasz model nadal działa i prawidłowo klasyfikuje zbiór testowy. W tym celu ładujemy zbiór MNIST, z którego interesuje nas jedynie zbiór testowy. Ponownie wybieramy jedynie zera i jedynki, bo nasz model potrafi rozpoznawać tylko te dwie cyfry. Zmieniamy kształt danych i normalizujemy je, a następnie wywołujemy metodę model.evaluate().

from keras.datasets import mnist

(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_test_new, y_test_new = x_test[(y_test==0) | (y_test==1)], y_test[(y_test==0) | (y_test==1)]

x_test_final = x_test_new.reshape((-1, 784)) / 255

eval = model.evaluate(x=x_test_final, y=y_test_new)
>>> 2115/2115 [==============================] - 0s 22us/sample - loss: 0.0065 - binary_accuracy: 0.9995
eval
>>> [0.006539232165791561, 0.9995272]

Wygląda na to, że model poprawnie się załadował i daje poprawne rezultaty na zbiorze jedynek i zer z MNIST.

A co gdybyśmy zrobili mały eksperyment na danych spoza MNIST? Pomyślałem, że wyrzeźbię obrazki z „odręcznie” zapisanymi zerem i jedynką, przetworzę je na formę zbliżoną do danych ze zbioru MNIST i zobaczę, co na to powie model. Celowo użyłem słowa „wyrzeźbię”, bo nie jestem biegły w programach graficznych ;-), a „odręczność” moich cyfr jest umowna, bo na narysowałem je myszą w Paint’cie, uprzednio ustalając wielkość tworzonego obrazka na 28 x 28 pikseli. Obrazki zapisałem na dysku jako bitmapę. Tak uzyskane pliki wymagają załadowania do tablicy numpy i konwersji na skalę szarości – patrz pierwsza linia kodu poniższej funkcji konwertującej (dla obu zadań potrzebowałem importowanej powyżej biblioteki PIL).

Niestety, konwersja z użyciem metody convert daje odwróconą skalę szarości. Tzn. tam gdzie w wartości określającej jasność piksela powinno być 0 jest 1 i odwrotnie. Stąd musiałem odjąć 1 i pomnożyć przez (-1). Dodatkowo w wyniku otrzymałem „ujemne zera” (wartości pokazywane jako -0.), stąd dla pewności funkcja abs() – patrz druga linia funkcji konwertującej. Zachęcam do powtórzenia mojego eksperymentu i narysowania swoich cyfr.

def convert_image(file):
   image = np.array(Image.open(file).convert('L'))
   return np.abs(((image / 255) - 1)*(-1))

Zobaczmy jak wygląda moje zero i czy jest dobrze klasyfikowane przez wyuczony przed chwilą klasyfikator.

im = convert_image(r'<<insert-full-path-here>>/moje-zero.bmp')
imshow(im)

predict_input = im.reshape((-1,784))
prediction = model.predict(predict_input)
prediction
>>> array([[0.00267569]], dtype=float32)

Wynik klasyfikacji (0.0027) jest bliski zeru, które dla mojego klasyfikatora oznacza akurat „zero”. A jaki wynik uzyskamy dla mojej „odręcznej” jedynki?

im = convert_image(r'<<insert-full-path-here>>/my-one.bmp')
imshow(im)

predict_input = im.reshape((-1,784))
prediction = model.predict(predict_input)
prediction
>>> array([[0.9701028]], dtype=float32)

Mamy tu 0.97, a więc dość pewną klasyfikację jako „jeden”. Wygląda więc na to, że klasyfikator zbudowany na bazie regresji logistycznej potrafił dość dobrze zgeneralizować problem i działa również poza zbiorem MNIST. Z czego bardzo się cieszę 🙂 .

Jeżeli ktoś chciałby poeksperymentować we własnym zakresie, to fajnym pomysłem wydaje się wybranie dwóch innych cyfr ze zbioru MNIST i sprawdzenie, czy można uzyskać podobne rezultaty. Ciekawe może być również narysowanie własnych odręcznych cyfr. A może zmiana funkcji logistycznej na tanh?

Mam nadzieję, że powyższy post przybliżył Wam zagadnienie regresji logistycznej do klasyfikacji binarnej z użyciem biblioteki Keras i że był on dla Was ciekawy.

---

Masz pytanie? Zadaj je w komentarzu.

Spodobał ci się post? Będzie mi miło, gdy go polecisz.

Do zobaczenia wkrótce, przy okazji omawiania innego ciekawego tematu!

---

Czy oglądasz mecze NBA? Sprawdź mój darmowy serwis NBA Games Ranked i ciesz się oglądaniem wyłącznie dobrych meczów.

---